这是一个钢琴八度。

结论：它可以被拓扑延展，如下图所示，得到一片叶子。

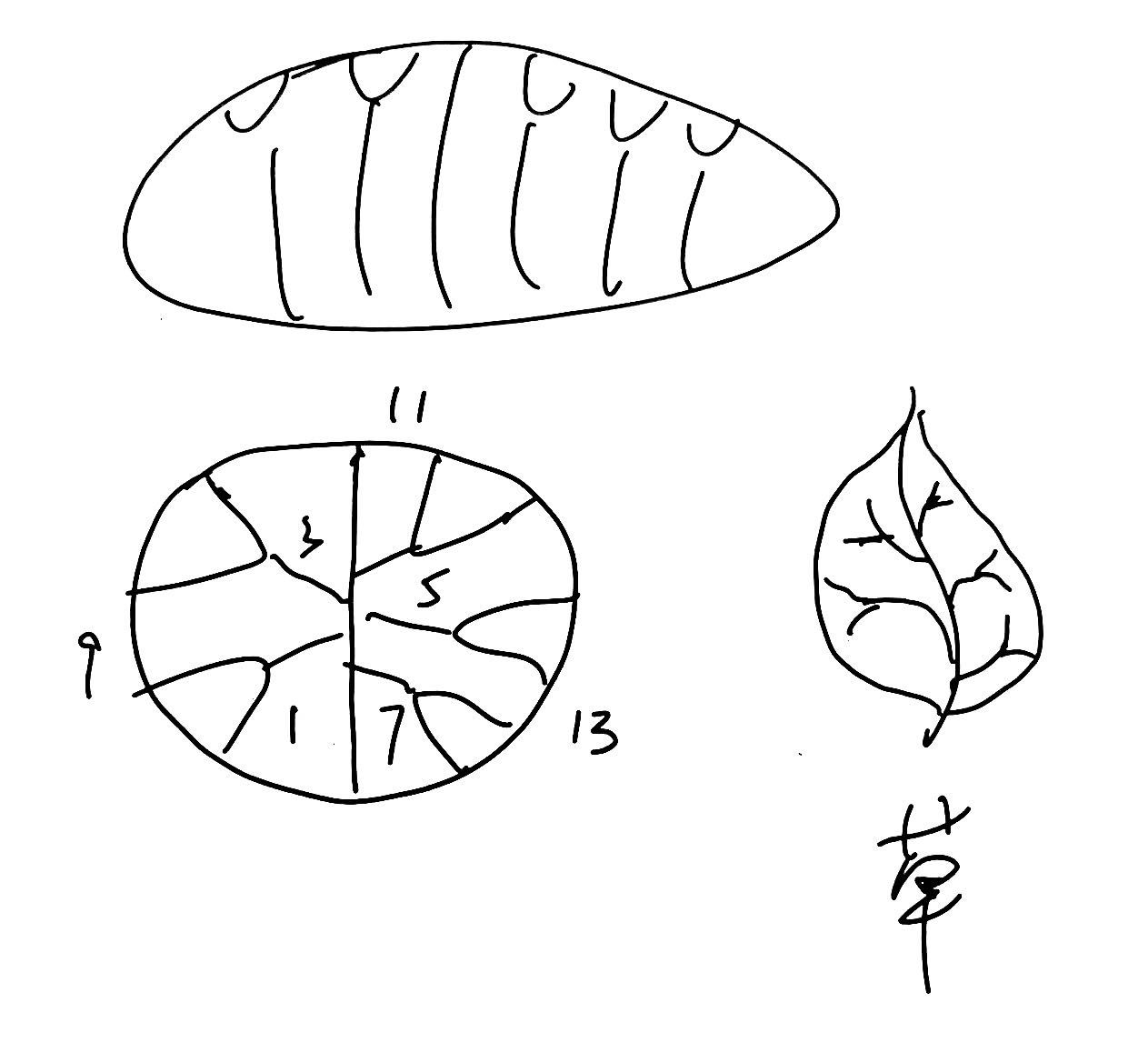
从直观的角度讲那么这个叶子的拓扑图示已经足够直观可以令人满意。这一拓扑成立的逻辑是乐器键的唱名与实际频率以对数关系进行匹配。详情参见四度圈。 下面是一些浅显的分析：

自然数列

一个钢琴图标有12个按键，7个白键，5个黑键。

如果我们将白键以中间mi.fa中线为分隔，将7个白键分为3和4。将得到这个富有美感的分隔：12=3+4+5。

   oo | ooo                                         这是黑键
  ooo | oooo                                        这是白键

如果我们往上补全，这就像是一个被稍微不对称切开的一个三角形：

      | #                                         以此类推（一个半音阶）
    # | ##                                        以此类推（一个sus2和弦）
   oo | ooo                                       这是黑键（一个五声音阶）
  ooo | oooo                                      这是白键（一个大调音阶）
 #### | #####
##### | ######

参见下面的分析过程

o/1 = 2                                             八度切1刀分为2部分
	 / \
   o/2 o\3          2+3=5                           这两部分分别切2刀和3刀分为3部分和4部分
   /     \
 'ooo'  'oooo'                                     

从对称角度看左边个数少了一个，把si放在左边

   # #    # # #
7 1 2 3  4 5 6

  oo    ooo
o ooo   ooo                                         同时上移

得到下面的图示

 # # #    # # #  ................tp1.1
  1 2 3  4 5 6

式tp1.1中，左上角#为主叶子（见后文），因此特标为$即:

 $ # #    # # #  ................tp1.2
  1 2 3  4 5 6

叶子$的左右位置直接决定了这个过程是否对称。 如果认为在左边，则分解对称。如果在右，则为对称破缺（我知道这是一个看起来很草率的解释，我可能并不知道破缺的真正物理含义，但至少在这里用起来很合理）。

我们将音程分解步骤对应下面的过程的一部分：

6=&5················6分
5=&4················5分
4=&3................4分
3=&2................3分
2=&1................2分
1=&0················

这是一个不断向上生长的图式。应该也可以做拓展。

其它结构

等角螺线

目前音高标准以440hz为标准音。实际可调，这个整体调律的过程可以看被可视化为一个在等角螺线上的12等分线旋转的过程。略

关于生命和音乐

所有生命都内置时钟。生命过程理论揭示了这一点。几乎从一开始生命就开始寻求另一半，不论是精神分析的所指还是就像那则古老的预言：人生来就是不完整的。 Robert M.May在1976发表的论文《Simple mathematical models with very complicated dynamics》这篇文章中就简化过这个过程:称为Logistic映射

$$ X_{t+1} = aX_t (1-X_t) $$

对称

对称的意义像折痕对于折纸，如果你对一个折叠起来的美丽折纸感到好奇，最好的方式是尝试重新沿着折痕拆开然后复原它。或者从时间上看，这是一个守恒量，证明了一些不变的东西。有些守恒量，人们以命运称之。

但如果你只想欣赏这幅作品，那就笑而不语。